Question

Determine the multiplicity of the zeros for the function f(X) = (x+2) (2x+5)

Answer 1

The multiplicity of roots refers to the number of times each root appears in a given polynomial. Determining the multiplicity of the roots of polynomials is easy if we have the factored version of the polynomial.

`f(x)=(x+2)(2x+5)`

The roots of the polynomial are

`\begin{gathered} x=-2\to(1) \\ \end{gathered}`
`\begin{gathered} 2x+5=0 \\ 2x=-5 \\ x=(-5)/(2)\to(2) \end{gathered}`

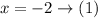
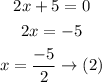
Both roots have multiplicity 1 that is to say that their multiplicity of the function must be the sum of both multiplicities in this case it would be 2

Graphically it looks like the following: