Question

At a point on the ground 80 ft from the base of a tree, the distance to the top of the tree is 11 ft more than 2 times the height of the tree. Find the height of the tree.The height of the tree is ___ ft(Simplify your answer. Round to the nearest foot as needed.)

Answer 1

Let h be the height of the tree and d the distance to the top of the tree from the point on the ground. Draw a diagram to visualize the situation:

Since the distance to the top of the tree is 11 ft more than two times the height, then:

`d=2h+11`

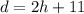
Use the Pythagorean Theorem to relate the length of the sides of the right triangle:

Notice that we have obtained a quadratic equation in terms of h. Write it in standard form and use the quadratic formula to solve for h:

`\begin{gathered} \Rightarrow0=4h^2+44h+121-h^2-6400 \\ \Rightarrow0=4h^2-h^2+44h+121-6400 \\ \Rightarrow0=3h^2+44h-6279 \\ \Rightarrow3h^2+44h-6279=0 \\ \\ \Rightarrow h=(-44\pm√((44)^2-4(3)(-6279)))/(2(3)) \\ \\ \therefore h_1=39 \\ h_2=-53.666.. \end{gathered}`

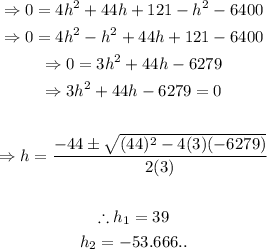
Since the height of the tree must be positive, the only solution is h=39ft. To the nearest foot, the height of the tree is 39.

Therefore, the height of the tree is 39 ft.