To classify each number as a rational or irrational number, first we need to define what a rational and irrational number is.
Rational numbers: are the ones that can be written in a fraction form, and that have periodic decimals (can be infinite decimals but they have to have a sequence to them).
Irrational number: are the ones that have infinite and non-periodic decimals (the decimals don't have a defined sequence)
Let's analyze each case.
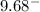
The bar on top of the number 8 represent that the number 8 repeats itself:

This decimals are infinite but they are periodic, which means that we have a defined sequence in this decimals (it will always follow the number 8). Thus, this is a rational number.
For the second number:
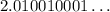
Since there is no sequence in the decimals in this case, this is an irrational number.
For the third number:
![\sqrt[\square]{64}](https://img.qammunity.org/2023/formulas/mathematics/college/qnl8bcu9aluj7f025dn7abyyhwc99dl0m6.png)
The square root of 64 is equal to 8:
![\sqrt[]{64}=8](https://img.qammunity.org/2023/formulas/mathematics/college/t9knwnrrfnspxz92nppspik0fsejfrwq3x.png)
and all the whole or integer numbers are also rational.
For the fourth number:
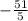
This is a rational number, because as we can see, it is represented in a decimal form which is a property of rational numbers.
For the last number:
![\sqrt[\square]{6}](https://img.qammunity.org/2023/formulas/mathematics/college/zotgwezaharsc2qnqemx4o52jcloeqyv8v.png)
and since this square root is not exact as the square root of option 3, this is an irrational number because:
![\sqrt[\square]{6}=2.4494897\ldots](https://img.qammunity.org/2023/formulas/mathematics/college/336s4m0ymvdomk7lyidlkmjsouubp4fd29.png)
Which are non-periodic decimals (without a defined sequence).