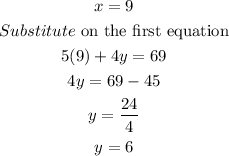Answer:
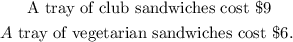
Explanation:
Given the information, create the following augmented matrix:
The first order was for 1 tray of club sandwiches, at a cost of $9. The second-order, which cost $69, was for 5 trays of club sandwiches and 4 trays of vegetarian sandwiches.
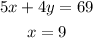
Into an augmented matrix:
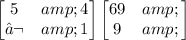
Solve.
Let x be the cost of a tray of club sandwiches.
Let y be the cost of a tray of vegetarian sandwiches.