Question

How canAllie determine the number of medium coffees she can buy with the gift card if she does not know the original value of the card?

Answer 1

Given two points, we can determine the equation of a line employing the next formula

`\begin{gathered} y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1_{}) \\ (x_1,y_1),(x_2,y_2)_{} \end{gathered}`

Where the last expression refers to two points on the line. Then, in our case

`\begin{gathered} (x_1,y_1)=(2,19.70),(x_2,y_2)=(4,14.40) \\ \Rightarrow y-19.70=(14.40-19.70)/(4-2)(x-2) \\ \Rightarrow y-19.70=-(5.3)/(2)(x-2) \end{gathered}`

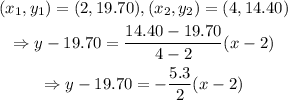
Where x represents the cups of coffee and y the gift card balance.

We are asked for the number of coffees she can buy in total using the gift card, in other words, the number of coffees she can get when the gift card balance reaches zero.

For this set y=0 and solve for x, as follows:

`\begin{gathered} 0-19.70=-(5.3)/(2)(x-2) \\ \Rightarrow-19.7\cdot2=-5.3(x-2) \\ \Rightarrow39.4=\text{5}.3x-10.6 \\ \Rightarrow50=5.3x \\ \Rightarrow x=9.4339\ldots \end{gathered}`

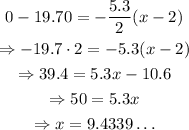
Then, she can buy no more than 9 coffees and some credit will remain on the gift card.