Answer::
![x=(2)/(√(e-1))\text{ or }x=-\frac{2}{\sqrt[]{e-1}}](https://img.qammunity.org/2023/formulas/mathematics/college/elj1rvgobpqzcug5si6e7dsajsxsr00o0z.png)
Step-by-step explanation:
Given the equation:
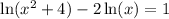
First, we can make the number 2 an index:

Apply the division law of logarithm to combine the left-hand side:
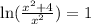
Take the exponent of both sides:
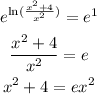
Solve the equation above for x:
![\begin{gathered} ex^2-x^2=4 \\ x^2(e-1)=4 \\ x^2=(4)/(e-1) \\ x=\pm\sqrt[]{(4)/(e-1)} \\ x=\pm\frac{2}{\sqrt[]{e-1}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/dn2hs6s8jvrds5tp0p5de84k4ioyyk6qpn.png)
The values of the variable x are:
![x=(2)/(√(e-1))\text{ or }x=-\frac{2}{\sqrt[]{e-1}}](https://img.qammunity.org/2023/formulas/mathematics/college/elj1rvgobpqzcug5si6e7dsajsxsr00o0z.png)