Question

Mrs. Welch and her 3 children are shopping at a local grocery store. Each of the children will be allowed to select one box of cereal for their own from the 10 different boxes of cereal available (there are no two the same). In how many ways can the selections be made?

Answer 1

The given information is:

- There are 3 children

- Each of the children will be allowed to select one box from the 10 different boxes of cereal available

- All the boxes are different

The number of ways the boxes can be selected n= 10!=10x9x8x7x6x5x4x3x2x1

The number of ways the 3 children can choose r= 3!=3x2x1

Here we have a permutation without repetition, because we have to reduce the options each time, so the formula is:

`P=(n!)/((n-r)!)`

If we replace n=10 and r=3, we obtain:

`P=(10!)/((10-3)!)=(10!)/(7!)=(10*9*8*7*6*5*4*3*2*1)/(7*6*5*4*3*2*1)=10*9*8=720`

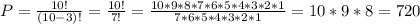
The answer is 720.