Question

To celebrate the upcoming Harvest Season, Ms. White takes a hot air balloon trip over the Temecula Valley, the San Bernardino Mountains, and the Coachella Valley with her teacher friends. They travel at an average speed of 65 mi/h for 97.5 miles before they land to take a 45-minute lunch break. After lunch, they fly 75 miles at an average speed of 50 mi/h before they have to land for a 20-minute bathroom break. They then rush back at 70 mi/h for 105 miles. Including the lunch & bathroom breaks, how many hours was their entire trip? Express your answer as a decimal to the nearest hundredth.

Answer 1

When we have the average speed and the distance, we can calculate the travel time as:

`v=(d)/(t)\Rightarrow t=(d)/(v)`

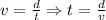
Then, we have to add the time of each scale.

a) 97.5 miles at 65mi/h:

`t=(d)/(v)=\frac{97.5\text{ mi}}{65\text{ mi/h}}=1.5\text{ h}`

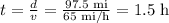
b) Lunch break: 45 min = 0.75 h

c) 75 miles at 50 mi/h:

`t=(d)/(v)=\frac{75\text{ mi}}{50\text{ mi/h}}=1.5\text{ h}`

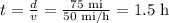
d) Bathroom break: 20 min = 0.33 h

e) 105 miles at 70 mi/h:

`t=(d)/(v)=\frac{105\text{ mi}}{70\text{ mi/h}}=1.5\text{ h}`

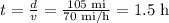
Then, we add all the hours for each stage and get:

`t=1.5+0.75+1.5+0.33+1.5=5.58`

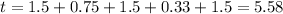
Answer: the entire trip took 5.58 hours.