ΔABC and ΔXYZ are similar triangles, then:
- The corresponding angles are equal
- The corresponding sides are at the same rate
You need to determine the length of ZX, so you have to work using the second property.
The corresponding sides are at the same ratio, this can be expressed as follows:
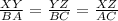
You can use
AC=13
ZX=N
BA=5
XY=1.25
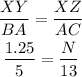
Multiply both sides by 13:
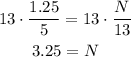
The length of ZX is 3.25 units.