1 Answer

Sephora · Answer 1 · 2023-06-10T22:01:36+0000

SOLUTION

Step1; Write out the set of data

7, 13, 8, 3, 11, 7, 14, 7, 18, 2

The mean is given as

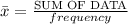
$\bar{x}=\frac{\text{SUM OF DATA}}{frequency}$
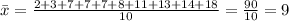
$\bar{x}=(2+3+7+7+7+8+11+13+14+18)/(10)=(90)/(10)=9$

The mean is 9.00

The variance of a set of data is given as

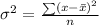
$\sigma^2=\frac{\sum (x-\bar{x})^2}{n}$

consider the table below

$\begin{gathered} (\sigma^2=(2-9)^2+(3-9)^2+(7-9)^2+(7-9)^2+(7-9)^2+(8-9)^2+(11-9)^2+(13-9)+(14-9)^2+(18-9)^2)/(10) \\ \end{gathered}$

Hence the variance becomes

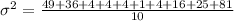
$\sigma^2=(49+36+4+4+4+1+4+16+25+81)/(10)_{}$
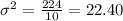
$\sigma^2=(224)/(10)=22.40$

The variance is 22.40

The standard deviation is given as

$\begin{gathered} \text{std}=\sqrt[]{variance} \\ \sigma=\sqrt[]{22.40}=4.73 \end{gathered}$

Please log in or register to add a comment.