Question

I need help solving this practiceThe answer options for the three boxes are located at the bottom of the picture One answer option per box

Answer 1

To answer this question we will use the following trigonometric identity:

`\sin^2\theta+\cos^2\theta=1.`

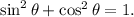
Solving the first equation for cosθ we get:

`\begin{gathered} x-2=4\cos\theta+2-2, \\ x-2=4\cos\theta, \\ (x-2)/(4)=(4\cos\theta)/(4), \\ (x-2)/(4)=\cos\theta. \end{gathered}`

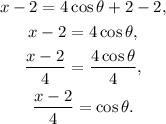
Solving the second equation for sinθ we get:

`\begin{gathered} y+5=2\sin\theta-5+5, \\ y+5=2\sin\theta, \\ (y+5)/(2)=(2\sin\theta)/(2) \\ (y+5)/(2)=\sin\theta. \end{gathered}`

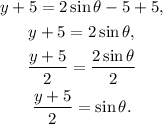
Substituting

`\cos\theta=(x-2)/(4)\text{ and }\sin\theta=(y+5)/(2)`

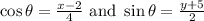
in the trigonometric identity we get:

`((x-2)/(4))^2+((y+5)/(2))^2=1.`

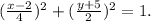
Simplifying the above result we get:

`((x-2)^2)/(16)+((y+5)^2)/(4)=1`

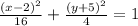
Finally, recall that:

`-1\leq\cos\theta\le1.`

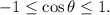
Therefore:

`\begin{gathered} -4+2\leq4\cos\theta+2\leq4+2, \\ -2\leq4\cos\theta+2\leq6. \end{gathered}`

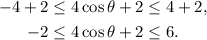
Therefore x is on the interval:

`[-2,6].`

Answer:

`((x-2)^2)/(16)+((y+5)^2)/(4)=1`

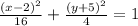
where x is on the interval

`[-2,6].`