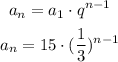Write the equation of the arithmetic and geometricsequences given 15, 5, ...a. arithmeticb. geometric

Question

asked May 27, 2023 138k views

1 Answer

Pdiddy · Answer 1 · 2023-06-02T10:05:21+0000

The rate in a arithmetic sequence can be determined by the subtraction of two subsequent terms:

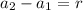
So, using the second term equal to 5 and the first one equal to 15, we have:

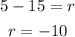
$\begin{gathered} 5-15=r \\ r=-10 \end{gathered}$

Now, using the formula for the nth term of a arithmetic sequence, we have:

$\begin{gathered} a_n=a_1+(n-1)\cdot r \\ a_n=15-10(n-1) \end{gathered}$

Now, for the geometric sequence, the rate is given by the division of two subsequent terms:

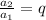
So we have that:

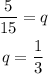
$\begin{gathered} (5)/(15)=q \\ q=(1)/(3) \end{gathered}$

The nth term of a geometric sequence is given by:

$\begin{gathered} a_n=a_1\cdot q^(n-1) \\ a_n=15\cdot((1)/(3))^(n-1) \end{gathered}$