What we have here in the picture is a graph of a segment. The goal is to find the segment's length, which we can do by using the distance formula:
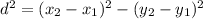
Note that the distance between two points is equal to the length of the line segment that joins them.
So now we already have answers for two of the boxes.
The difference in the x-coordinates gives us the horizontal distance between the two points, while the difference in the y-coordinates gives us the vertical distance between the points.
So, the other two boxes should contain: