We have a data set with size 8.
We have to find the minimum, the first quartile, median, the third quartile and the maximum.
To find this values, we have to first sort the data set from least to greatest:
{30, 36, 46, 50, 51, 73, 80, 91}
We can then identify the minimum and the maximum.
The minimum value is 30 and the maximum is 91.
The median will be the value for which 50% of the data is blow that value and 50% is above.
In this case, as the size is 8, the median will be the average between the 4th and the 5th value.
We then can calculate the median as:
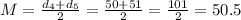
The quartiles are similar to the median, but the percentages of the data above and below change. In fact, the median is the second quartile.
The firts quartile Q1 has 25% of the data below and 75% of the data above its value.
In this case, 25% of the data is 2 data points, so it will be the average of the 2nd and 3rd point:
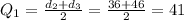
The third quartile Q3 has 75% of the data below and 25% above, so it can be calculated as the average between the 6th and the 7th data point:
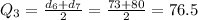
Answer:
Minimum = 30
Q1 = 41
Median = 50.5
Q3 = 76.5
Maximum = 91