Question

Help me answer this. Have in mind i’m in a rush!

Answer 1

vertex for function 1 : (-2,4)

vertex for function 2: (2,7)

function 1 has the smaller value

it is 4

Step-by-step explanation

given

`f(x)=ax^2+bx+c`

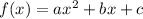
to get the vertex from the quadratic function we need to use

`\begin{gathered} h=-(b)/(2a) \\ so \\ \text{vertex} \\ (h,f(h)) \end{gathered}`

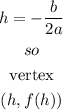
then

Let

Step 1

Function 2

Let

`\begin{gathered} f(x)=3x^2-12x+19\Rightarrow ax^2+bx+c \\ \text{hence. a=3 b=-12} \\ h=-(b)/(2a) \\ h=-(-12)/(2(3))=(12)/(6)=2 \\ \text{now, f(h), so} \\ f(2)=3(2)^2-12(2)+19 \\ f(2)=12-24+19=31-24=7 \end{gathered}`

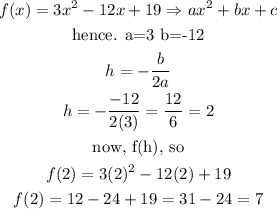
hence, the vertex is

vertex: (2,7)

Step 2

function 1

we have the table, so

a) find the function

so

for x= 1

`\begin{gathered} f(x)=ax^2+bx+c \\ f(1)=a(1)^2+b(1)+c \\ f(1)=a+b+c \\ \text{ in the table we have ( 1,7) so} \\ 7=a+b+c\Rightarrow equation(1) \end{gathered}`

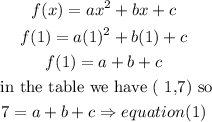
for x= -2

`\begin{gathered} f(x)=ax^2+bx+c \\ f(-2)=a(-2)^2+b(-2)+c \\ f(-2)=4a-2b+c \\ \text{ in the table we have ( -2,4) so} \\ 4=4a-2b+c\Rightarrow equation(2) \end{gathered}`

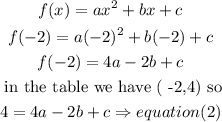
for x= 4

`\begin{gathered} f(x)=ax^2+bx+c \\ f(4)=a(4)^2+b(4)+c \\ f(4)=16a+4b+c \\ \text{ in the table we have ( 4,16) so} \\ 16=16a+4b+c\Rightarrow equation(3) \end{gathered}`

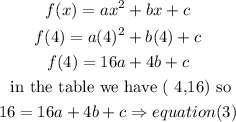
now, we have a system of 3 variables and 3 equations, so

`\begin{gathered} 7=a+b+c\Rightarrow equation(1) \\ 4=4a-2b+c\Rightarrow equation(2) \\ 16=16a+4b+c\Rightarrow equation(3) \end{gathered}`

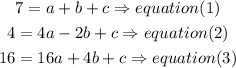
a) subtract equation (2) from equation (1) to eliminate c

`\begin{gathered} 7=a+b+c\Rightarrow equation(1) \\ -(4=4a-2b+c)\Rightarrow equation(2) \\ _(--------------) \\ 3=-3a+3b\Rightarrow equation(4) \end{gathered}`

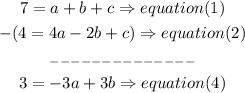
b) subtract eq(3) from eq(1) to eliminate c

`\begin{gathered} 7=a+b+c\Rightarrow equation(1) \\ -(16=16a+4b+c) \\ _(--------------) \\ -9=-15a-3b\Rightarrow equation\text{ (5)} \end{gathered}`

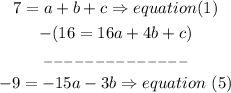
c) now, add equation (4) and equation(5) to eliminate b

`\begin{gathered} 3=-3a+3b\Rightarrow equation(4) \\ -9=-15a-3b\Rightarrow equation\text{ (5)} \\ ----------- \\ -6=-18a \\ \text{divide both sides by -18} \\ (-6)/(-18)=(-18a)/(-18) \\ (1)/(3)=a \end{gathered}`

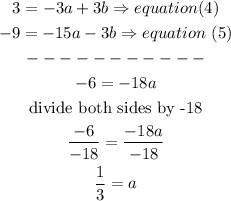
now, replace in equation (4) to find b

`\begin{gathered} 3=-3a+3b\Rightarrow equation(4) \\ 3=-3((1)/(3))+3b\Rightarrow equation(4) \\ 3=-1+3b \\ \text{add}1\text{ in both sides} \\ 3+1=-1+3b+1 \\ 4=3b \\ \text{divide both sides by 3} \\ (4)/(3)=b \end{gathered}`

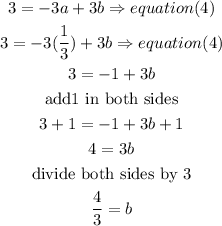
d) finally, replace a and b values into equation (1) , then solve for c

`\begin{gathered} 7=a+b+c\Rightarrow equation(1) \\ 7=(1)/(3)+(4)/(3)+c\Rightarrow equation(1) \\ 7=(5)/(3)+c \\ \text{subtract 5/3 in both sides} \\ (21)/(3)-(5)/(3)=c \\ (16)/(3)=C \end{gathered}`

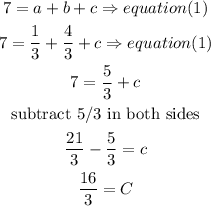
hence, the function is

`\begin{gathered} f(x)=ax^2+bx+c \\ f(x)=(1)/(3)x^2+(4)/(3)x+(16)/(3) \end{gathered}`

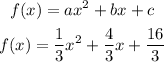
now, apply the formula to find the vertex

`\begin{gathered} f(x)=(1)/(3)x^2+(4)/(3)x+(16)/(3)\Rightarrow ax^2+bx+c \\ \text{hence. a=1/3 b=}\frac{\text{4}}{3} \\ h=-((4)/(3))/(2((1)/(3)))=((4)/(3))/((2)/(3))=-(12)/(6)=-2 \\ h=-2 \\ \text{now, f(h), so} \\ f(-2)=(1)/(3)(-2)^2+(4)/(3)(-2)+(16)/(3) \\ f(-2)=(4)/(3)-(8)/(3)+(16)/(3)=(12)/(3)=4 \\ so,\text{ the vertex is } \\ (-2,4) \end{gathered}`

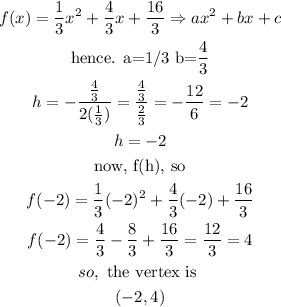
vertex for function 1 : (-2,4)

Step 3

smaller minimum value:

let's compare the image of the vertex

vertex for function 1 : (-2,4)

vertex for function 2: (2,7)

the y coordinate the function 2 is greater, so

function 1 has the smaller value

it is 4

I hope this helps you