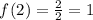Question

Consider the functionf (x) = x · In (x2)Find f"(2)

Answer 1

Derivatives

We are given the function

`f(x)=x\cdot\ln (x^2)`

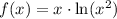
We must find

`f^(\doubleprime)(2)`

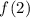
Or the second derivative of f evaluated at x=2.

Find the first derivative. We must recall the following rules of derivatives:

`\begin{gathered} \lbrack f\cdot g\rbrack^(\prime)=f^(\prime)\cdot g+f\cdot g^(\prime) \\ (\ln u)^(\prime)=(u^(\prime))/(u) \\ (x^n)^(\prime)=n\cdot x^(n-1) \end{gathered}`

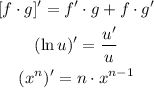
Let's compute f'(x):compute

`\begin{gathered} f^(\prime)(x)=(x)^(\prime)\cdot\ln x^2+x\cdot(\ln x^2)^(\prime) \\ f^(\prime)(x)=(1)\cdot\ln x^2+x\cdot(2x)/(x^2) \\ f^(\prime)(x)=\ln x^2+2 \end{gathered}`

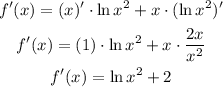
Now take the derivative again:

`\begin{gathered} f^(\doubleprime)(x)=(\ln x^2+2)^(\prime) \\ f^(\doubleprime)(x)=(2x)/(x^2)+0=(2)/(x) \end{gathered}`

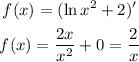
Evaluating at x=2:

`f^(\doubleprime)(2)=(2)/(2)=1`