Question

what are the measures of angle 1 and angle 2? < 1 = 58.2°, m<2= 75.51= 67.4 2= 104.51= 75.5 2=67.41= 104 2= 58.2

Answer 1

The shape in the picture is composed of two triangles and you have to determine the measures of ∠1 and ∠2.

Let's start by calculating the measure of ∠2, to do so we have to work with the lower triangle:

To calculate the measure of ∠2 we have to apply the external angle theorem, this theorem states that the measure of the external angle of a triangle is equal to the sum of the two opposite inner angles of the said triangle, so that:

`17.3º+\angle2=121.8º`

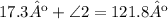
From this expression, we can determine the measure of ∠2, just subtract 17.3 from both sides of the expression:

`\begin{gathered} 17.3-17.3+\angle2=121.8-17.3 \\ \angle2=104.5º \end{gathered}`

Now, ∠2 is a linear pair with one of the base angles of the upper triangle, which means that they add up to 180º:

`\begin{gathered} \angle2+xº=180º \\ 104.5+x=180º \end{gathered}`

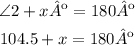
Subtract the measure of ∠2 from 180º to determine its supplementary angle:

`x=180-104.5=75.5º`

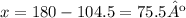
Finally, now that we know two out of the three angles of the triangle, we can determine the measure of ∠1 as follows:

`\angle1+37.1+75.5=180º`
`\begin{gathered} \angle1+112.6=180 \\ \angle1=180-112.6 \\ \angle1=67.4º \end{gathered}`

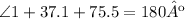
So

∠1= 67.4º and ∠2= 104.5º, the correct option is the second one.