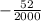Question

A quintic polynomial function (degree of five) with zeros x1=-4 (order 2), x2=5 (order 3), and y-intercept at 52 as shown. What is the leading coefficient

Answer 1

Step-by-step explanation:

The roots of the qunitic polynomial is given below as

`\begin{gathered} x_1=-4(order2) \\ x_2=5(order3) \\ y-intercept=52 \end{gathered}`

The general form of a plolynomial is given below as

`y=a(x-n)(x-m)(x-p)`

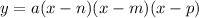
In this case,

the equation will be given below as

`y=a(x+4)^2(x-5)^3`

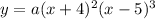
To apply the intercepts, we will use the coordinates below to find the value of a

`(0,52)`
`\begin{gathered} y=a(x+4)^(2)(x-5)^(3) \\ 52=a(4^2)(-5)^3 \\ 52=-2000a \\ divide\text{ both sides by -2000} \\ a=-(52)/(2000) \\ a= \end{gathered}`

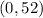
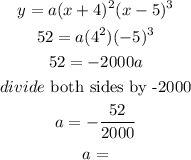
Hence,

The leading coefficient will be

`-(52)/(2000)`