Question

5 points

The following graph shows the radioactive decay curve for lodine-131. A
patient administered 50 grams of iodine-131. Use the graph (and your
equations) to determine how many grams of this radioactive isotope will
remain in the body after 32 days? Be sure you answer has 2 significant
figures. Show/Attach ALL YOUR WORK for full credit.
100
Decay of Iodine-131
BO
50
Percent of Iodine-131 Remaining
40
20
16
Number of Days
1 Add file

Answer 1

First, we have that on day 0, the percent of remaining iodine is 100%. This percent reaches 50% on day 8; so the half-life of iodine-131 is 8 days.

With this data, we can find the remaining amount based on the following formula:

`N(t)=N_o\cdot((1)/(2))^{\frac{t}{half-life_{}}}\begin{cases}N_o=initial\text{ quantity} \\ t=\text{time (days)} \\ half-life=half-life\text{ (days)}\end{cases},^{}^{}`

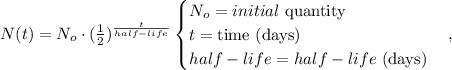
We have that the initial quantity is 50 grams and the time is 32 days. Replacing all data, we obtain:

`N(t)=50\cdot((1)/(2))^{(32)/(8)}=50\cdot((1)/(2))^4=(25)/(8)=3.125\text{ g.}`

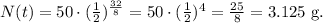
So, the remaining quantity of iodine-131 after 32 days is 3.1 grams.