We are given the following three sides of a triangle.
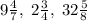
We are asked to find the perimeter of the triangle.
Recall that the perimeter of a triangle is the sum of all three sides.
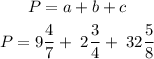
Add the whole parts and the fractions separately,
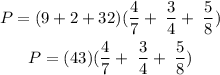
The LCM of 7, 4, 8 is 56
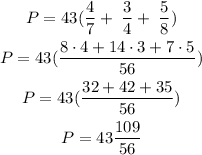
Therefore, the perimeter of the triangle in the mixed form is 43 109/56 yards