Question

AIB Assignments Give the information asked for to each problems 3 In each of the following state the Start Value Growth Value Calendar 5/9 1. -f + 32 CH 4000 FEE 2. y = 4000 - 250x ... 3. X -3 O 3 6 у -9 -5 -1 3 4. х -4 4 8 y 3 9 15 21 5. A financial account begins with $5000. Each week $300 is deducted. 6. Also point to the start value Apps Help Type here to search gi e MO

Answer 1

The start value of a function is the y-intercept of the function, f(x=0).

1. C(f=0)=8/9f+32

C(f=0)=32 --> the start value of the function

Growth value would be 8/9, because it's a linear function and that's the constant rate of change.

2. In this case, is exactly the same analysis:

y=4000-250x

Start value of the function would 4000 because it's the output value when x=0, that means the y-intercept. And the growth value would be -250 because it's the rate of change of the linear function.

3. Since we have the value tables, we can create the equation of the linear function:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(-5-(-9))/(0-(-3))=(4)/(3) \\ y+3=m(x+9) \\ y=(4)/(3)x+12-3 \\ y=(4)/(3)x+9 \end{gathered}`

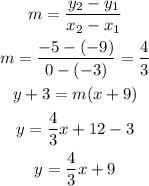
By that, the start value of the function would be y(0)=9, and the growth value would be 4/3

4. We can do the same thing with the other value table:

`\begin{gathered} m=(9-3)/(0-(-4))=(3)/(2) \\ y-3=(3)/(2)(x+4) \\ y=(3)/(2)x+6+3 \\ y=(3)/(2)x+9 \end{gathered}`

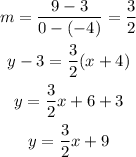
The start value of the function would be y(0)=9, and the growth value would be 3/2