Given that,
y = ln(7x^2 - 5x + 6)
Now, we have to calculate the derivative of that. The derivative of ln(x) can be written as:
y' = 1/x * d/dx
hence, we can write the above equation as:
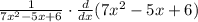
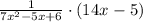
As d/dx(x^n) = nx^(n-1)
and
d/dx (constant) = 0
Hence,
y' = (14x-5)/ (7x^2 - 5x + 6)