Question

For the sequence an=3−5⋅(n−1) ,its first term is ;its second term is ;its third term is ;its fourth term is ;its fifth term is ;its common difference d= .

Answer 1

Given an explicit formula for an arithmetic sequence below

`a_n=3-5\cdot(n-1)`

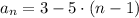
For the first term,

Where n = 1

`\begin{gathered} a_1=3-5\cdot(1-1)=3-5(0)=3-0=3 \\ a_1=3 \end{gathered}`

Hence, the first term is 3

For the second term

`\begin{gathered} a_n=3-5\cdot(n-1) \\ a_2=3-5(2-1)=3-5(1)=3-5=-2 \\ a_2=-2 \end{gathered}`

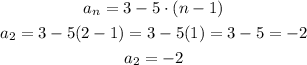
Hence, the second term is -2

For the third term

`\begin{gathered} a_(n)=3-5(n-1) \\ a_3=3-5(3-1)=3-5(2)=3-10=-7 \\ a_3=-7 \end{gathered}`

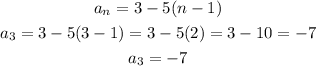
Hence, the third term is -7

For the fourth term

`\begin{gathered} a_(n)=3-5(n-1) \\ a_4=3-5(4-1)=3-5(3)=3-15=-12 \\ a_4=-12 \end{gathered}`

Hence, the fourth term is -12

For the fifth term

`\begin{gathered} a_(n)=3-5(n-1) \\ a_5=3-5(5-1)=3-5(4)=3-20=-17 \\ a_5=-17 \end{gathered}`

Hence, the fifth term is -17

For the common difference, d,

`\begin{gathered} d=second\text{ term}-first\text{ term} \\ d=a_2-a_1=-2-3=-5 \\ d=-5 \end{gathered}`

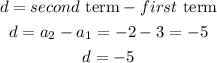
Hence, the common difference, d, is -5