Solve the problem. Suppose that P dollars in principal is invested in an account earning 5.3% interest compounded continuously. At the end of 3 yr, the amount in the account has earned $1,378.70 in interest. Find the original principal. Round to the nearest dollar.
we know that
The formula to calculate continuously compounded interest is equal to

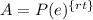
where
A is the Final Investment Value
I is the interest
P is the Principal amount of money to be invested
r is the rate of interest in decimal
t is Number of Time Periods
e is the mathematical constant number
we have
r=5.3%=0.053
t=3 years
I=$1,378.70
substitute the given values in the formula
Remember that
A=I+P=1,378.70+P
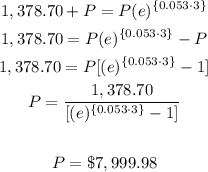
Round to the whole number
P=$8,000