Question

This assessment has been due 2 weeks ago and i don't understand it

Answer 1

i) m =5

ii) y +6 = 5(x + 2)

iii) y = 5x +4

Step-by-step explanation:

The points on your work: (-2, -6) and (1, 9)

we apply the slope formula:

`m\text{ = }(y_2-y_1)/(x_2-x_1)`
`\begin{gathered} x_1=-2,y_1=-6,x_2=1,y_2\text{ = }9 \\ m\text{ = }(9-(-6))/(1-(-2))=(9+6)/(1+2)=(15)/(3) \\ m\text{ = 5} \end{gathered}`

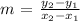
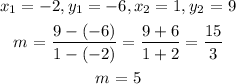
The point slope formula:

`y-y_1=m(x-x_1)`

we can use any of the points given for x1 and y1. Let's go with the one used above where x1 = -2 and y1 = -6

`\begin{gathered} y\text{ - }(-6)\text{ = 5(x - (-2))} \\ Point\text{ slope formula: }y\text{ +6 = 5(x + 2)} \end{gathered}`

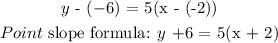
Slope intercept form:

y = mx + c

we need to find c which is the y-intercept

using any points above: (-2, -6) = (x, y)

Insert the point into the formula as (x, y) to get c

-6 = 5(-2) + c

-6 = -10 + c

-6+10 = c

c = 4

Slope intercept form: y = 5x + 4