Question

Find the intercepts and the vertical and horizontal asymptotes, and then use them to sketch a graph of the function. f(x)=x+2/x^2−16

Answer 1

We have the function:

`f(x)=x+(2)/(x^2)-16.`

We must find:

0. the intercepts,

,

1. the vertical and horizontal asymptotes.

1) x-intercepts

The x-intercepts are given by the x values such that f(x) = 0. So we must find the values of x that satisfies the equation:

`f(x)=x+(2)/(x^2)-16=0.`

Solving for x, we get:

`\begin{gathered} x+(2)/(x^2)-16=0 \\ x\cdot x^2+2-16\cdot x^2,\text{ }x\\e0, \\ x^3-16x^2+2=0. \end{gathered}`

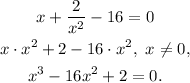
The real roots of this equation are:

`\begin{gathered} x_1\approx15.9922, \\ x_2\approx0.35757, \\ x_3\approx-0.34975. \end{gathered}`

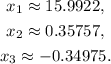
So the x-intercepts are the points:

`\begin{gathered} P_1=(15.9922,0), \\ P_2=(0.35757,0), \\ P_3=(-0.34975,0)\text{.} \end{gathered}`

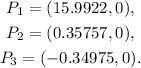
2) y-intercepts

The y-intercepts are given by the y values such that x = 0. Replacing x = 0 in the definition f(x), we see that the denominator of the second term diverges. So we conclude that there are no y-intercepts.

3) Vertical asymptotes

Vertical asymptotes are vertical lines near which the function grows without bound. From point 2, we know that the function grows without limit when x goes to zero. So one vertical asymptote is:

`x=0.`

4) Horizontal asymptotes

Horizontal asymptotes are horizontal lines that the graph of the function approaches when x → ±∞. We consider the limit of the function f(x) when x → ±∞:

`\lim _(x\rightarrow\pm\infty)f(x)=\lim _(x\rightarrow\pm\infty)(x+(2)/(x^2)-16)\rightarrow\pm\infty.`

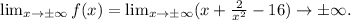
We see that the function does not tend to any constant value when x → ±∞. So we conclude that there are no horizontal asymptotes.

5) Oblique asymptotes

When a linear asymptote is not parallel to the x- or y-axis, it is called an oblique asymptote or slant asymptote.

A function ƒ(x) is asymptotic to the straight line y = mx + n (m ≠ 0) if

`{\displaystyle\lim _(x\to+\infty)\mleft[f(x)-(mx+n)\mright]=0\, {\mbox{ or }}\lim _(x\to-\infty)\mleft[f(x)-(mx+n)\mright]=0.}`

We consider the line given by:

`y=mx+n=x-16.`

We compute the limit:

`\begin{gathered} \lim _(x\rightarrow\pm\infty)(f(x)-(x-16)) \\ =\lim _(x\rightarrow\pm\infty)((x+(2)/(x^2)-16)-(x-16)) \\ =\lim _(x\rightarrow\pm\infty)((2)/(x^2)) \\ =0. \end{gathered}`

So we have proven that f(x) has the oblique asymptote:

`y=x-16.`

6) Graph

Plotting the intercepts and the asymptotes, we get the following graph:

Answer

1) x-intercepts: (-0.34975, 0), (0.35757, 0), (15.9922, 0)

2) y-intercepts: none

3) Vertical asymptotes: x = 0

4) Horizontal asymptotes: none

5) Oblique asympsotes: y = x -16

6) Graph