Answer:
D. y = (x – 2)(x – 4)(x + 3)
Explanation:
We want to completely factor the polynomial.
First, given the division of polynomials below:
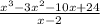
To use synthetic division, set the denominator equal to 0 and solve for x:

Next, write the result(2) outside and the coefficients of the numerator inside as shown below:
Carry down the leading coefficient as shown below:
Multiply the carry down value(1) by the number outside (2) and write the number under the next column:
Repeat until it gets to the last column:
Therefore:
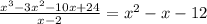
We factor the resulting quadratic expression:
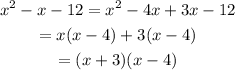
So, we have:
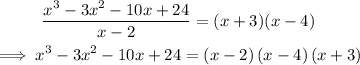
Thus:
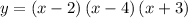
Option D is correct.