Add the total percentage of households that have two or more televisions, then, calculate the number of households by multiplying 250 by the corresponding percentage. Then, find the total amount of households with less than two televisions and substract those quantities to find how many more are there with two or more televisions than those with less than two televisions.
The percentage of households with two televisions is 23%, with three televisions is 24%, for four televisions is 13% and 6% have five or more. Then, the total percentage of households with two or more televisions, is:
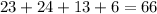
Since 66% of 250 households have two or more televisions, then the number of households in that category, is:
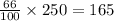
The percentage of households with less than two televisions is equal to:
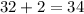
The number of households with less than two televisions, is:
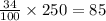
Therefore, the difference from households with two or more televisions and those with less than two televisions, is:
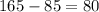
The, there are 80 more households that have two or more televisions than those with less than two televisions.