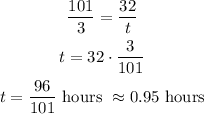The rate of completed problems can be calculated using the equation:
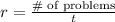
Then, for Adrian and Abbi:
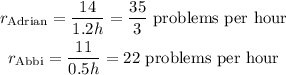
If they work together, the total rate will be the sum of the individual rates:
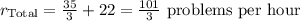
We know the rate and the number of problems (32), so using the equation for the rate: