Question

A door delivery florist wishes to estimate the proportion of people in his city that will purchase his flowers. Suppose the true proportion is 0.05. If 304 are sampled, what is the probability that the sample proportion will differ from the population proportion by more than 0.037

Answer 1

The variable of interest is:

X: number of people in the city that purchase the florist flowers, out of 304 people.

This variable has a binomial distribution with parameter n=304 and p=0.5

The population proportion of people that buys his flowers is

p=0.5

You have to calculate the probability that the sample proportion will differ from the population proportion by more than 0.037, that is

P(p.hat>p+0.037)

To calculate this probability, given that the sample size is big enough, you have to approximate the distribution of the sample proportion to normal by applying the Central Limit Theorem.

Using this approximation the sample proportion will have a normal distribution with mean "np" and variance [p(1-p)]/n

So that:

`\text{p\lbrack{}hat\rbrack}\approx N(np,(p(1-p))/(n))`

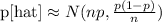
If you subtract for the value of p[hat] its mean and divide it by its standard deviation, you'll be able to standardize its value (transform it into a Z-value)

`Z=\frac{p\lbrack hat\rbrack-np}{\sqrt[]{(p(1-p))/(n)}}\approx N(0,1)`

Using this formula you can calculate the asked probability.

P(p[hat]>p+0.037)

P(p[hat]>0.5+0.037)

P(p[hat]>0.537)

To transform it into a value of Z you have to calculate the mean and standard deviation of the distribution of p[hat]

Mean