Question

• For the reaction2N2O(g) → 4NO2(g) + O2(g)the rate of formation of NO2(g) is 2.8x10-3 M/sCalculate the rate of disappearance of N2O5 (g).

Answer 1

2N2O5(g) → 4NO2(g) + O2(g) (this is our reaction and it is already balanced)

2 moles N2O5 disappears (reactant)

4 moles NO2 appears (product)

We can work with equations here that represent the disappearance and appearance of compounds:

The disappearance of N2O5: rate of disappearance

`-(1)/(2)(d\lbrack N_2O_5\rbrack)/(dt)`

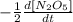
The appearance of NO2: rate of appearance

`+(1)/(4)\frac{d\lbrack N_{}O_2\rbrack}{dt}`

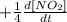
We can do this:

`-(1)/(2)(d\lbrack N_2O_5\rbrack)/(dt)=\text{ }+(1)/(4)\frac{d\lbrack N_{}O_2\rbrack}{dt}`

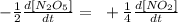
We can do this because the disappearance of reactants involves the appearance of the product.

Then, we clear the rate of N2O5:

`-(d\lbrack N_2O_5\rbrack)/(dt)=2x(1)/(4)\frac{d\lbrack N_{}O_2\rbrack}{dt}=(1)/(2)x2.8x10^(-3)(M)/(s)=1.4x10^(-3)(M)/(s)`

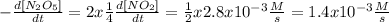
Now the rate of disappearance of N2O5 = 1.4x10^-3 M/s