Question

In the diagram below, if the measure of ∠∠C = 45 °, and side AB = 12√3, then side BC =

Answer 1

Given:

∠C = 45°

AB = 12√3

For us to be able to get the measure of side BC, we will be using the Tangent Function:

`\text{ Tangent }\Theta\text{ = }\frac{\text{ Opposite }}{\text{ Adjacent}}`

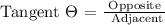
Where,

Θ = ∠C = 45°

Opposite = AB = 12√3

Adjacent = BC

We get,

`\text{ Tangent \lparen45}^(\circ))\text{ = }\frac{\text{ 12}\sqrt{3\text{ }}}{\text{ BC}}`
`\text{ BC = }\frac{\text{ 12}\sqrt{3\text{ }}}{\text{ Tangent \lparen45}^(\circ))}`
`\text{ BC= }\frac{\text{ 12}√(3)}{\text{ 1}}\text{ = 12}√(3)`

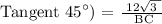
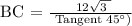
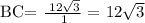
Therefore, the answer of BC is 12√3, the triangle is an isosceles triangle.

The answer is CHOICE C.