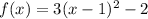ANSWER
The axis of symmetry is x = 1
The vertex form is
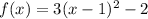
Step-by-step explanation
The axis of symmetry is a vertical line through the vertex of the parabola. This vertical line has te value of the x-coordinate of the vertex, which is:
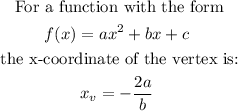
For this problem a = 3 and b = -6:
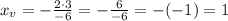
To write the equation in vertex form we have to find also the y-coordinate of the vertex. This is the value of the function when we replace x by xv:
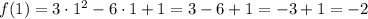
Therefore the vertex is at point (1, -2).
The vertex form of a quadratic equation is:

So for this function, the vertex form is: