Ok to probe that ABD=CBD you need to prove that:

To prove that you have to use the Pythagorean theorem which states that given a rigth triangle abc with c as its hypotenuse:
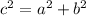
In this problem AB and BC are the hypotenuses of triangles ABD and CBD respectively. So you have to use the theorem in both:
![AB=\sqrt[]{(AD)^2+(BD)^2}\text{ }](https://img.qammunity.org/2023/formulas/mathematics/college/agz1rxk6pm7dc0av0p8exkkvoes3v7yp9a.png)
![BC=\sqrt[]{(DC)^2+(BD)^2}\cong\sqrt[]{(AD)^2+(BD)^2}=AB](https://img.qammunity.org/2023/formulas/mathematics/college/jy24b4y9ybfhpl09q19j4etwgm3648rlof.png)
So in step 3 the type of statement would be:

And the reason would be: according to the pythagorean theorem
The last step would be step 4 and the statement would be:

The reason: they