Question

Answer the questions regarding the graph of F. Then use this information to graph the function.

Answer 1

(a)

Rises to the left and rises to the right

(b)

Zero(s) where the graph crosses the x-axis: 0, 1

Zero(s) where the graph touches, but does not cross the x-axis: -2

(c)

The y-intercept of the graph of f is 0

(d)

Explanation:

We have the following polynomial function:

`\begin{gathered} f\mleft(x\mright)=x\mleft(x-1\mright)\mleft(x+2\mright)^2 \\ f(x)=x^4+3x^3-4x \end{gathered}`

We can observe from the function that degree is even (4) and leading coefficient is positive(+1), which means that the behavior of the function would be:

Rises to the left and rises to the right

To know the zeros of the function, we must equal the function to 0, therefore it would remain:

`\begin{gathered} x(x-1)(x+2)^2=0 \\ x=0 \\ x-1=0\rightarrow x=1 \\ (x+2)^2=0\rightarrow x+2=0\rightarrow x=-2 \end{gathered}`

Zero(s) where the graph crosses the x-axis: 0, 1

Zero(s) where the graph touches, but does not cross the x-axis: -2

(c)

We have that y-intercept, we calculate it when x is equal to 0, therefore:

`\begin{gathered} f(x)=0\cdot(0-1)\cdot(0+2)^2 \\ f(x)=0 \\ y=0 \end{gathered}`

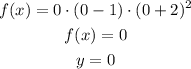
The y-intercept of the graph of f is 0

(d)

The resulting graph would be (obtained by means of a graphics program, for better understanding):