Given
Jake rewrote the equation of the surface area of a Cylinder as it is solved for h as it is shown in the figure.
To find the error made by Jake.
Now,
The surface area of the cylinder is given by,
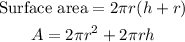
Subtracting both sides with
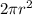
Implies,
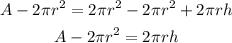
Dividing both sides by
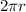
gives,
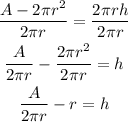
Comparing the above solution for h and the solution of h in the figure, we get the error in the last step as Jake didn't simplify the left side correctly.
Hence, the error is c) On the last step, Jake didn't simplify the left side correctly.