Answer = 125 minutes
Assuming that the customers uses x minutes in a month.
The first plan can be represented as :
• 20+ 0.19x ....... equation 1 .
The second plan can be represented as :
• 25 +0.15x ....equation 2
When we equate both equation , we ca find the minutes of call of two plans :
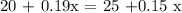
Solving the above equation, we get that :
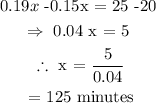
This means that, for 125 minutes , both option will be equal.