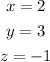To solve the system of equations:
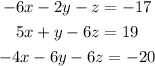
We need to choose two sets of two equations and eliminate the same variable from those to get a 2 by 2 system that we can solve. If we choose the first and second equation and multiply the first one by -6 we get:
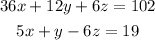
Now we add the equation to get:
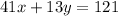
Now we choose the second and third equation and change the sign of the second equations, then we get:
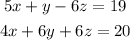
Adding them we have:
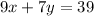
Now we have the system:
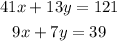
To solve it we mutiply the first equation by 7 and the second one by -13, then we have:
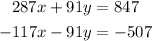
Adding this equation we have:
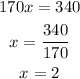
Now that we have the value of x we plug it in the second equation for the 2 by 2 system to get y:
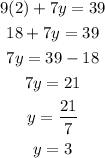
Finally to find z we plug the value of x and y in the first equation of the original 3 by 3 system, then:
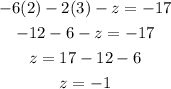
Therefore the solution of the system is: