To obtain the equation of the line that passes through these points, you can first obtain the slope of the line, using the formula
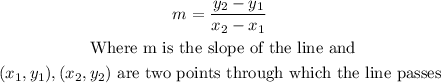
And then use the point-slope formula

So, in this case, you have
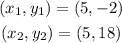
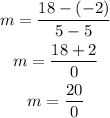
Since the division by 0 is an indeterminacy then the slope of this line is not defined and these points pass through a vertical line that passes through x = 5, as you can see in the graph
Therefore, the slope of the line is undefined and the equation of the line that passes through these pair of points is
