Question

The admission fee at an amusement park is $3.25 for children and $4.80 for adults. On a certain day, 284 people entered the park, and the admission fees collected totaled $1109. How many children and how many adults were admitted?

Answer 1

Given: The admission fee at an amusement park is $3.25 for children and $4.80 for adults

To Determine: How many children and how many adults were admitted if the total money collected is $1109

Solution

Let x be number of children and y be the number of adults

So,

`\begin{gathered} equation1:x+y=284 \\ equation2:3.25x+4.80y=1109 \end{gathered}`

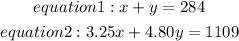
Solve for x and y

`\begin{gathered} from\text{ equation 1} \\ equation3:x=284-y \end{gathered}`

Substitute x in equation 2

`\begin{gathered} 3.25(284-y)+4.80y=1109 \\ 923-3.25y+4.80y=1109 \\ 923+1.55y=1109 \end{gathered}`
`\begin{gathered} 1.55y=1109-923 \\ 1.55y=186 \\ y=(186)/(1.55) \\ y=120 \end{gathered}`

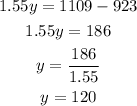
Substitute y in equation 3

`\begin{gathered} x=284-y \\ x=284-120 \\ x=164 \end{gathered}`

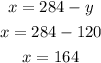
Hence, there are 164 children and 120 adults