Question

BD is the altitiude to △ABC, ∠A=6x-1, ∠ABD=9x+1, and ∠C=5x-5. Find the value of x and the measure of ∠DBC.

Answer 1

Given:

BDis the altitude of triangle ABC.

So,

`\angle BDA=90^0`

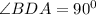
The other angles are,

`\begin{gathered} \angle A=6x-1 \\ \angle ABD=9x+1 \\ \angle C=5x-5 \end{gathered}`

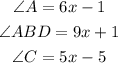
The objective is to find the value of x and the angle CBD. Let's take angle CBD as y.

First consider, triangle ABD.

Sum of angles of a triangle is 180 degree.

`\begin{gathered} \angle A+\angle ABD+\angle D=180 \\ 6x-1+9x+1+90=180 \\ 15x+90=180 \\ 15x=180-90 \\ 15x=90 \\ x=(90)/(15) \\ x=6 \end{gathered}`

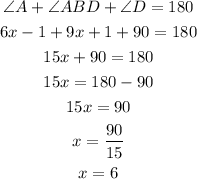
Hence, the value of x is 6.

Now consider the triangle ABC.

`\begin{gathered} \angle A+\angle ABD+\angle DBC+\angle C=180^0 \\ 6x-1+9x+1+y+5x-5=180 \\ 20x+y-5=180 \\ 20x+y=180-5 \\ 20x+y=175 \end{gathered}`

Now, substitue the value of x.

`\begin{gathered} 20(6)+y=180 \\ 120+y=180 \\ y=180-120 \\ y=60^0 \end{gathered}`

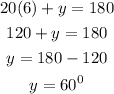
Hence,

The value of x is 6.

The value of angle CBD is 60 degree.