Question

help me determine the values of the variables that will make f continuous everywhere for E and F please

Answer 1

A function is said to be continuous when it does not have any abrupt changes in output values.

E.

For f(x) to be continuous the function should be defined smoothly, i.e. it should not have any holes.

Now, we know that f(x) = 5 when x ≤ 2 and f(x) = ax+b for 2 < x < 4. Therefore, we must choose a and b such that

`\lim _(n\to2^+)ax+b=2`

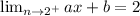
and

`\lim _(n\to4^-)ax+b=11`

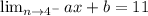
The first equation gives

`2a+b=2`

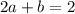
and the second equation gives

`4a+b=11`

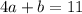
This is now a system of two equations and we solve it by first solving for b in the first equation and substituting its value in the second equation.

The first equation gives

`b=2-2a`

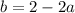
putting that into the second equation gives

`4a+2-2a=11`
`\rightarrow2a+2=11`
`\begin{gathered} \rightarrow2a=9 \\ \therefore a=4.5 \end{gathered}`

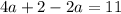
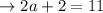
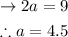
And the value of b is

`\begin{gathered} b=2-2a \\ b=2-2(4.5) \end{gathered}`
`\therefore b=-7.`

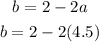
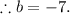
Hence, a = 4.5 and b = -7 will make f(x) continuous.

F).

Using the same logic as above, we find that the must satisfy the following limits if it is to be continuous.

`\lim _(n\to1^+)ax^2=7x`

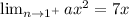
and

`\lim _(n\to3^-)ax^2=bx+3`

The first equation gives

a(1)^2 = 7(1)

a = 7

and the second equation gives

a(3)^2=b(3) + 3

`9(7)=3b+b3`
`63=3b+3`

`\therefore b=20.\text{ }`

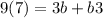
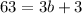
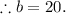
Hence, a = 7 and b = 20 make f(x) continuous.