First let's see the expression for a geometric series:
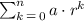
In this problem r=4 and n=8. a is not given, however, you do have the second term of the series:
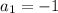
This means that, when k=1, the term equals 1:
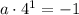
So, we can figure out the value of a from here:
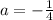
So, the complete geometric series given is:
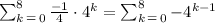
And finally you just have to evaluate the sum:
