ANSWER
Quotient = p + 7
Remainder = 10
Step-by-step explanation
We want to solve by long division:
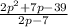
To do this we have:
![\begin{gathered} \text{Divide each term in the polynomial by 2p and multiply by -7:} \\ \text{ p} \\ 2p-7\sqrt[]{2p^2+7p-39} \\ \text{ - (2p}^2\text{ - 7p)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/lqai8tgq6v0ei0tb2t6gzqeahddea2sh4f.png)
Subtract the lower polynomial from the higher one and repeat the process:
![\begin{gathered} \text{ p + 7} \\ 2p-7\text{ }\sqrt[]{2p^2+7p-39} \\ \text{ - (2p}^2\text{ - 7p) } \\ \Rightarrow14p-39\text{ (-39 is from the original expression)} \\ \text{-(14p - 49) (subtract from the expression above)} \\ \text{ =}>\text{ 10} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nuikdnnzii3bkp90sbm53fu5snjsls7xkv.png)
Therefore, the result of the division is:
Quotient = p + 7
Remainder = 10