Question

4. One person at the top of a waterfall that is 90 feet tall dumps into the water. The distance from the person to the water can be modeled by the equation h= -16t^2 + s, where h is the height from the water, t is the time in seconds, and s is the initial height from the water in feet. How long will it take for the person to reach the water? Round your answer to the nearest tenth of a second.

Answer 1

2.37 sec

Step-by-step explanation

Step 1

`h=-16t^2+s`

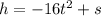
where

h is the height from the water, t is the time in seconds, and s is the initial height from the water in feet

then

Let

t=unknow

h=0(the person touch the water)

s=90 ft

now, replace

`\begin{gathered} h=-16t^2+s \\ 0=-16t^2+90 \\ \text{subtract 90 in both sides} \\ 0-90=-16t^2+90-90 \\ -90=-16t^2 \\ \text{Multiply both sides by -1} \\ -90\cdot-1=-16t^2\cdot-1 \\ 90=16t^2 \\ \text{divide both sides by 16} \\ (90)/(16)=(16t^2)/(16) \\ 5.625=t^2 \\ \text{square root in both sides} \\ \sqrt[]{5.625}=\sqrt[]{t^2} \\ 2.37=t \end{gathered}`

so, it will take 2.37 seconds to reach the water