Let the other number be represented by y.
Now, since the sum of the two numbers is 44, we have that:
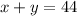
Now, we simply make y the subject of the relation by subtracting x from both sides of the equality sign, as follows:
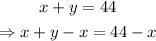
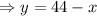
Therefore, the other number is given by:
