Notice that
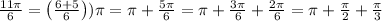
Then, angle 11pi/6 terminates within quadrant 4. As for its reference angle, notice that pi/3 radians is equivalent to 60°; then,
Thus, the reference angle is equal to
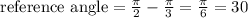
The reference angle of 11pi/6 is 30°.
Regarding angle 4pi/3, notice that
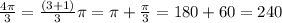
Then, 4pi/3 radians is equal to 240°