Question

Solve the equation. 2+|t+6|=12A: [4, -11]B: [4,11]C:[-16,4]D:[-4,16]

Answer 1

Given the expression:

`2+|t+6|=12`

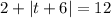
We can simplify it before using the definition of absolute value:

`\begin{gathered} |t+6|=12-2=10 \\ \Rightarrow|t+6|=10 \end{gathered}`

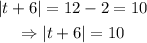
Now, following the definition of absolute value, we have the following:

`\begin{gathered} |a|=\mleft\{\begin{aligned}a,a\ge0 \\ -a,a<0\end{aligned}\mright. \\ \Rightarrow|t+6|=\mleft\{\begin{aligned}t+6,t+6\ge0 \\ -(t+6),t+6<0\end{aligned}\mright. \end{gathered}`

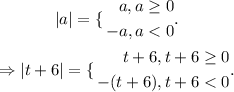
We first suppose that t+6>=0, then:

`\begin{gathered} t+6\ge0 \\ \Rightarrow t+6=10 \\ \Rightarrow t=10-6=4 \\ t=4 \end{gathered}`

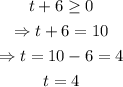
Now we take the case where t+6<0:

`\begin{gathered} t+6<0 \\ \Rightarrow-(t+6)=10 \\ \Rightarrow-t-6=10 \\ \Rightarrow-t=10+6=16 \\ \Rightarrow-t=16 \\ t=-16 \end{gathered}`

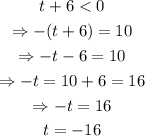
Therefore, the values of t that makes the expression 2+|t+6|=12 are -16 and 4.