Question

1. Write the equation of the line with a slope of -3 that passes through the point (1,9).y=3x + 12 y=3x +6y=-3x + 6 y=-3x+12

Answer 1

Let's begin by identifying key information given to us:

The general equation of a straight line is represented by the equation:

`\begin{gathered} y=mx+b \\ where\colon m=slope,b=x-intercept \end{gathered}`

The equation has a slope of -3. Hence, the equation becomes:

`\begin{gathered} y=mx+b \\ m=-3 \\ \Rightarrow y=-3x+b \end{gathered}`

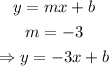
We were given that equation passed through the point (1, 9)

Since we were given one point, we will use the point-slope equation to obtain the equation of this straight line. We have it thus:

`\begin{gathered} y-y_1=m(x-x_1) \\ (x_1,y_1)=(1,9) \\ y-9=-3(x-1) \\ y-9=-3x+3 \\ \text{Add ''9'' to both sides, we have:} \\ y-9+9=-3x+3+9 \\ y=-3x+12 \end{gathered}`

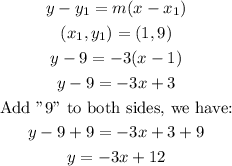
Therefore, the equation of the straight line is: y = -3x + 12