Take into account that the momentum is given by:
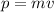
where m is the mass and v the speed of motion.
In order to calculate p it is necessary to find the value of v. Use the following expression for the kinetic energy:
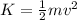
In this case, you have:
K = 64J
m = 2 kg
Solve for v and replace the previous values:
![\begin{gathered} v=\sqrt{(2K)/(m)} \\ v=\sqrt[]{\frac{2(64J)}{2\operatorname{kg}}}=8(m)/(s) \end{gathered}]()
Now, replace the value of v and m to find the momentum:
![p=(2kg)(8(m)/(s))=16\operatorname{kg}\cdot(m)/(s)]()
Hence, the momentum is 16 kg*m/s